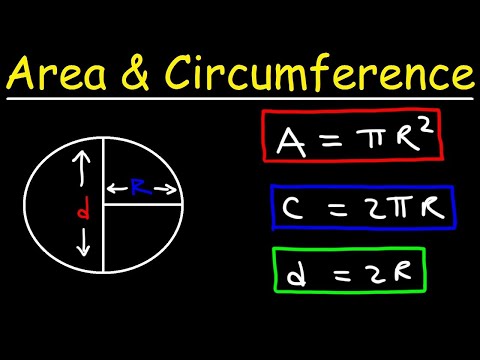
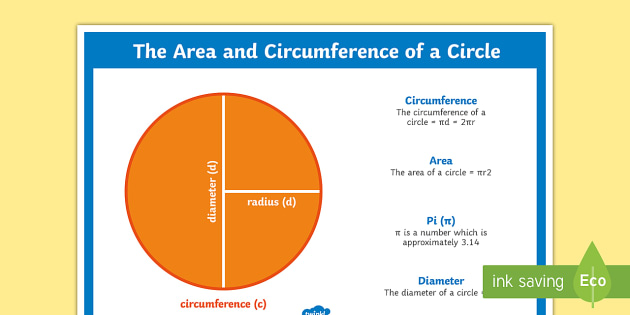
A circle is a geometric form of which every point on the outside of the circle is the same distance away from the center. The distance around the edge of the circle is called the circumference. The distance from one side of the circle to the other, going through the center of the circle, is the diameter. The constant pi, designated by the Greek letter π, is the ratio of the circumference to the diameter of a circle.
For any circle, if you divide the circumference by the diameter you get pi, an irregular number usually rounded to 3.14. To calculate the diameter of a circle, multiply the radius by 2. If you don't have the radius, divide the circumference of the circle by π to get the diameter. If you don't have the radius or the circumference, divide the area of the circle by π and then find that number's square root to get the radius. Then, you can just multiply the radius by 2 to find the circle's diameter.
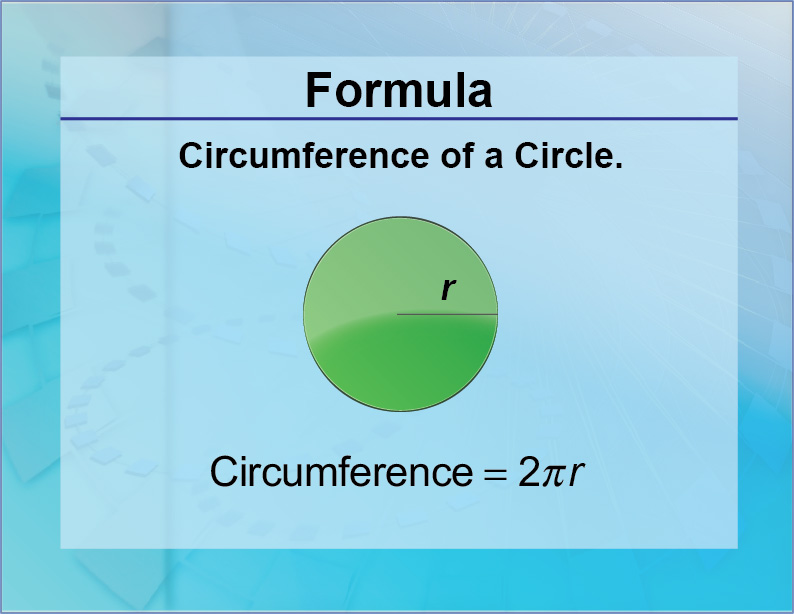
The formula for calculating the circumference of a circle from the diameter of a circle is very easy. Simply multiply the diameter by the number 3.14, which is also called the number pi (π). The answer will be in the units of length by which the diameter is measured. Blame Welsh mathematician William Jones for the trouble pi causes you.
In 1706 Jones used the Greek word for circumference, περιϕέρεια, and shortened it to its first letter, π. As for π in circles, we have no one to blame but the marvel that is mathematics. Pi, or π, is the irrational number that links every circle's circumference to diameter and radius. Life is full of circles (and semi-circles). Therefore, the equation of the circumference of a circle can be useful in solving any problem involving circles. Since circumference is a measurement of length, there are generally two main kinds of problems that will involve calculating the circumference of something circular.
First, knowing the circumference of a circle can be used to create something circular. Second, if the circle is moving at a known speed, then the circumference can be used to determine how far the circle might travel in a given time. The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle.
The diameter cuts the circle into two equal parts, which is called a semi-circle. For example, the length of a 180 degree arc must be half the circumference of the circle, the product of pi and the radius. The length of any arc is equal to whatever fraction of a full rotation the arc spans multiplied by the circumference of the circle. A 45 degree arc, for example, spans one-eighth of a full rotation, and is therefore equal to one-eighth the circumference of that circle.
The length of an arc of n degrees equals (n/360) times the circumference. The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference.
The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. You can also think of the radius as the distance between the center of the circle and its edge. Using geometrical formulas and equations gets easier with practice. Ask for help from someone who has worked with circles or any other geometrical figures.
You're likely to find that questions of geometry will seem less challenging with a little experience. Fizzywoz - If you look at examples #1-#4 at the end of the article you can see how numbers are plugged into the equation. You will usually just plug in a known radius into the equation to figure out the circumference or you may plug in a known circumference to determine the radius. Let me know if you have any other questions. As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape.
The circumference of a circle is the same as the length of a straight line folded or bent to make the circle. The circumference of a circle is measured in meters, kilometers, yards, inches, etc. Once again in this example, we're given the radius of the circle.
Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye.
While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? When we use the formula to calculate the circumference of the circle, then the radius of the circle is taken into account. Hence, we need to know the value of the radius or the diameter to evaluate the perimeter of the circle.
The diameter is defined as twice the length of the radius of a circle. There are infinite points on the circumference of a circle, this means that a circle has an infinite number of diameters, and each diameter of the circle is of equal length. If you know the circumference, radius, or diameter of a circle, you can also find its area.
Area represents the space enclosed within a circle. It's given in units of distance squared, such as cm2 or m2. The circumference of a circle is equal to pi times the diameter. Learn the circumference equation and definition.
See examples of how to calculate circumference when given the diameter or radius. Π shows the ratio of the perimeter of a circle to the diameter. Therefore, when you divide the circumference by the diameter for any circle, you obtain a value close enough to π. This relationship can be explained by the formula mentioned below.
Pi (π) is a special mathematical constant; it is the ratio of circumference to diameter of any circle. Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle. Whereas the area of circle defines the region occupied by it. If we open a circle and make a straight line out of it, then its length is the circumference. It is usually measured in units, such as cm or unit m. You can think of it as the line that defines the shape.
For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference. Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions. To calculate the circumference of a circular shape when the diameter is given we need to use the formula for circumference. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae.
The two semi-circles that form the remainder of the perimeter, and can be considered two halves of one circle. The circumference of the circle would account for the outer edges of the two semi-circles in the ice rink. Find the circumference of the circle with the formula as follows. For any circle, its circumference ratio to its diameter is equal to a constant known as pi. The distance around a polygon, such as a square or a rectangle, is called the perimeter . On the other hand, the distance around a circle is referred to as the circumference .
Therefore, the circumference of a circle is the linear distance of an edge of the circle. The circumference of the circular water pit is 18 feet. How can Marcus use this information to determine how long the beam needs to be to go across the center of the pit? Marcus needs to figure out the diameter of the pit. The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference .
The circumference of a circle is related to one of the most important mathematical constants. This constant, pi, is represented by the Greek letter π . Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference.
We know that the diameter of a circle is twice the radius. The proportion between the circumference of a circle and its diameter is equal to the value of Pi(π). Hence, we say that this proportion is the definition of the constant π.
Diameter Of A Circle Formula Using Circumference The diameter of a circle can be calculated according to the given parameters. If the parameters like radius, circumference, or area are given then we can directly use the following formulas. The circumference of a circle is merely the distance around a circle. Sometimes it is referred to as the perimeter, although the term perimeter is usually reserved for the measure of a distance around a polygon. One other key relationship, radius to diameter, can also give you circumference. Radius is one half of a circle's diameter.
This means we can substitute radius, r, in our formulas, using the substitution property of equality. If two radii are equivalent to one diameter, we can substitute diameter with 2r. In this concept, you will learn to find the diameter or radius of a circle given the circumference. She uses the formula for the circumference of a circle to calculate the diameter of Planet X.
Real-life Problem 2 – Planet X A new satellite is launched from a space station. The radius of a circle is the length of a single, straight line segment that connects the center of the circle to any one point on its edge. Use this circle calculator to find the area, circumference, radius or diameter of a circle. Given any one variable A, C, r or d of a circle you can calculate the other three unknowns. The term circumference is used when measuring physical objects, as well as when considering abstract geometric forms.
But, what if we aren't given either of these values? In order to solve for either the radius or diameter of a circle, we need to know either its circumference or its area. Now, let's take the circle with the diameter of 9 cm, and radius of 4.5 cm, and calculate the circumference. The circumference of a circle is defined as the linear distance around it. In other words, if a circle is opened to form a straight line, then the length of that line will be the circle's circumference. Thus, we can define three different formulas to find the perimeter of circle (i.e. circumference of a circle).
Circumference of a circle" or "Perimeter of circle" with its definition, formula, methods to find the circle's circumference with many solved examples. In fact, here comes the standard definition of \(\pi\) as the ratio of circumference and diameter of a circle. The diameter to circumference calculator is an online tool used to determine the value of the circumference of a circle. In the diameter to circumference calculator enter the dimension of the diameter and get the value of circumference within a few seconds. You can also try the diameter calculator for direct calculations.
Circumference refers to the enclosed boundary of the circle. It is also known as the perimeter of the circle. We can derive the diameter formula from the circumference and the radius of the circle. Since a circle's circumference is the linear distance of the circle's edge, it describes a length.
Therefore, the most common units of a circle's circumference are millimeter, centimeter, meter for the metric system, and inch, feet, and yard for the imperial system. The radius is one-half the diameter or it can be measured from the origin of the circle out to its edge. Where d is the diameter of the circle, r is its radius, and π is pi. Formulas are the key to getting things done in Excel. You'll also learn how to troubleshoot, trace errors, and fix problems.
The Excel PI function returns the value of the geometric constant π . The value represents a half-rotation in the radian angle system. The constant appears in many formulas relating the circle, such as the area of a circle. I don't know the type of measurement for your daughter's specific math problem, but whatever it is,those units would also squared.
Check out 4 common types of geometry homework problems and solutions involving the circumference of circles. Understanding what the circumference of a circle is, as well as how to calculate the circumference of a circle is a relatively easy geometry principle. By following the circumference problems and solutions in the Geometry Help Online section below, you should easily be able grasp the concept of circumference.







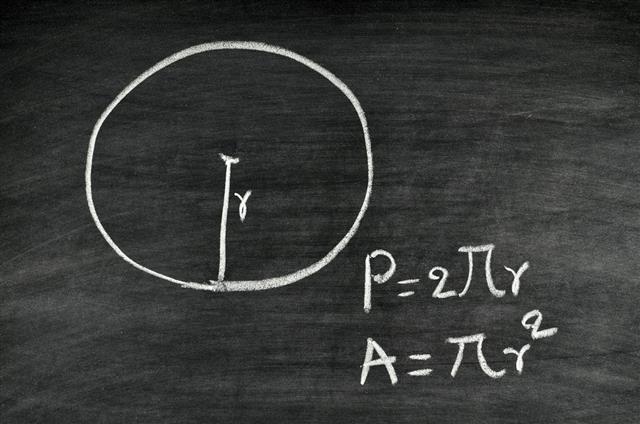
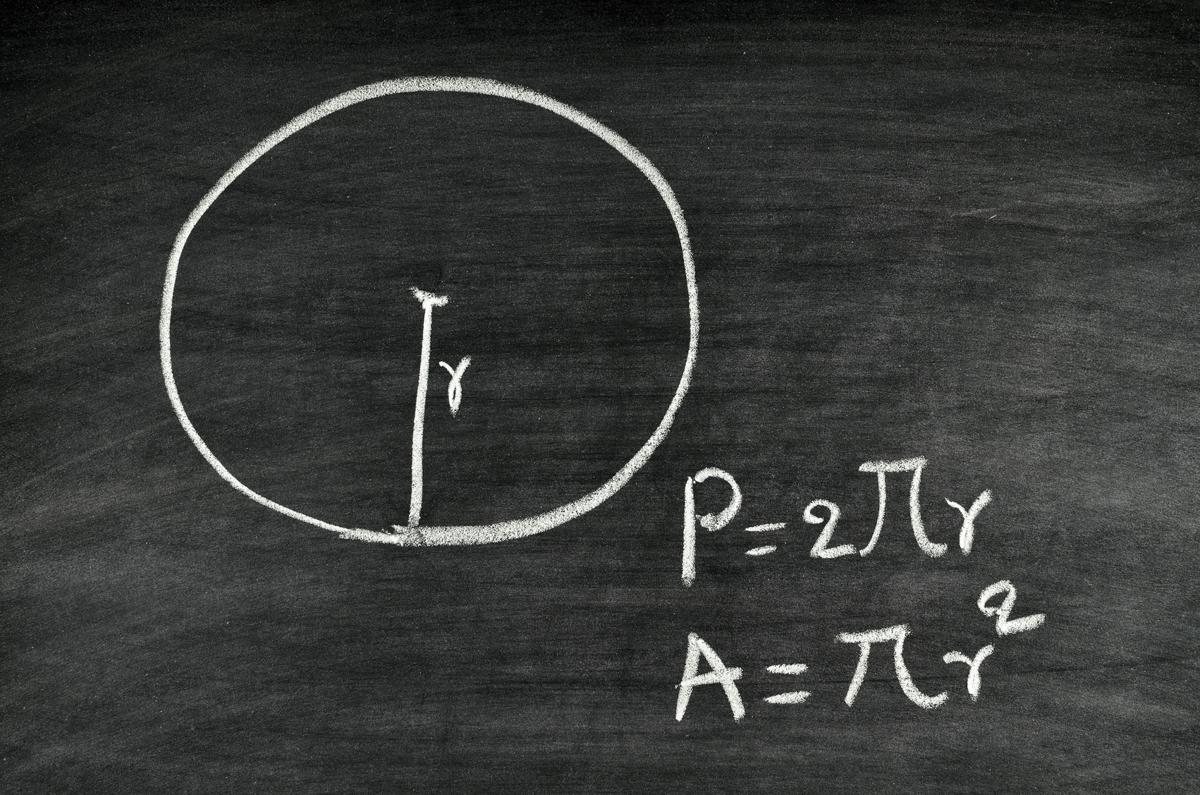













No comments:
Post a Comment
Note: Only a member of this blog may post a comment.